OPERACIONES CON POLINOMIOS
SUMA DE POLINOMIOS CON COEFICIENTES FRACCIONARIOS
RESTA DE POLINOMIOS CON COEFICIENTES FRACCIONARIOS
MULTIPLICACIÓN DE POLINOMIOS
CASO I. MULTIPLICACIÓN DE MONOMIOS
PASOS:
- Se multiplican los coeficientes numéricos, teniendo en cuenta la ley de los signos para la multiplicación.
- En la parte literal, se aplica el concepto de producto de potencias de igual base, que consiste en sumar los exponentes de las bases iguales y escribir la misma base.
Ejemplos:
VIDEO 1
VIDEO 2
TALLER. MULTIPLICACIÓN DE MONOMIOS
CASO II. MULTIPLICACIÓN DE MONOMIO POR POLINOMIO
Procedimiento:
1. Se multiplica cada uno de los terminos del polinomio por el monomio, en el siguiente orden:
a. Se multiplican los signos, teniendo presente la "Ley de los signos"
b. Se multiplican los coeficientes numéricos.
c. Se multiplica la parte literal. Cada letra particular representa una base; y, el producto de varias potencias con igual base se obtiene escribiendo la base común y, sumando los exponentes respectivos.
2. Se ordena el polinomio resultante.
EJEMPLOS:
(2x2)(5x3) = 10x5
(−3y4)(2y2)
= −6y6
(3xy5)(−6x4 y2) = −18x5 y7
(−12a2 b3 c4)(−3a2
b2) = 36a4 b5 c4
3(x2+3x−5) =3x2+9x−15
4x(3x2 −7) = 12x3 −28x
−7y(4y2 −2y+1) = −28y3 + 14y2
− 7y
2x3 (−3x4 + 2x3 − 10x2 +7x + 9) = −6x7 + 4x6 − 20x5 + 14x4 + 18x3
−7a2 b c3 (5a2 −3b2
−9c2 ) = −35a4 b c3 +21a2 b3
c3 + 63a2 b c5
VIDEO 1
VIDEO 2
VIDEO 3
VIDEO 4
CASO III. MULTIPLICACIÓN DE POLINOMIOS POR POLINOMIOS
PASOS:
- Se multiplica el primer término de un polinomio, por todos los términos del otro polinomio
- Se multiplica el segundo término de un polinomio, por todos los términos del otro polinomio
- Se multiplica el tercer término de un polinomio, por todos los términos del otro polinomio
- Y así sucesivamente…
- Se reagrupan términos, sumando y restando los términos semejantes
EJEMPLO 1:
1. Multiplicamos el primer término del primer polinomio, por todos los términos del segundo polinomio:
2. Ahora, multiplicamos el segundo término del primer polinomio, por todos los términos del segundo polinomio:
3. Agrupamos los términos semejantes:
EJEMPLO 2:
1. Multiplicamos el primer término del primer polinomio por todos los términos del otro polinomio:
2. Multiplicamos el segundo término del primer polinomio por todos los términos del otro polinomio:
3. Multiplicamos el tercer término del primer polinomio por todos los términos del otro polinomio:
4. Agrupamos términos semejantes:
VIDEO 1
VIDEO 2
VIDEO 3
TALLER: MULTIPLICACIÓN DE POLINOMIOS POR POLINOMIOS
DIVISIÓN DE POLINOMIOS
CASO I. División de monomios
Procedimiento:
1. Se aplica la ley de los signos.
2. Se divide el coeficiente del dividendo entre el coeficiente del divisor.
3. Se divide la parte literal del dividendo entre la parte literal del divisor, teniendo en cuenta la ley de los exponentes "para dividir potencias de la misma base se escribe la base común con exponente igual a la diferencia entre el exponente del dividendo y el exponente del divisor".
4. En el cociente se escribe primero el signo, seguido del coeficiente numérico y, por último, la parte literal en orden alfabético.
Ejemplo1:
Se organizan los monomios de la siguiente manera y se aplican los pasos indicados en el procedimiento.
Ejemplo4:
Ejemplo2:
Ejemplo3:
Ejemplo4:
TALLER DIVISIÓN MONOMIO ENTRE MONOMIO
CASO II. División de polinomio entre monomio
Para dividir un polinomio entre un monomio, dividimos cada término del polinomio por el monomio. Ejemplos:
CASO III. División de polinomio entre polinomio
Procedimiento:
1. Se ordenan los dos polinomios en orden descendente.
2. Si en el polinomio dividendo, hacen falta términos, se completan esas casillas con ceros.
3. Se halla el cociente entre el primer término del dividendo y el primer término del divisor y se escribe en el cociente.
4. Este resultado se multiplica por cada uno de los términos del divisor y el resultado se resta del dividendo.
5. Se bajan los términos siguientes.
6. Se repite nuevamente el proceso hasta que el polinomio del residuo sea de menor grado que el polinomio del divisor o sea cero.
Ejemplo 1.
(X2 + 2X – 3) ÷ (X+3)
Ejemplo 2.
(– 2X4 +
3X2 – 1) ÷ (X2 – X + 1)
Ejemplo 3.
(a2 – 5a – 6) ÷ ( a – 3)
Ejemplo 4.
Ejemplo 5.
















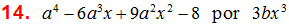












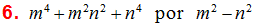



































Comentarios
Publicar un comentario